偽隨機函數 (Pseudorandom Functions)
Goldreich、Goldwasser 和 Micali (GGM) [GGM84] 引入的 偽隨機函數 (PRFs) 是對稱鑰匙密碼學的基石。一個 PRF 族是一個函數集合 ，由索引 s（通常稱為 密鑰 或 種子 (seed)）標識，將一個公共的有限定義域映射到一個公共的有限值域。其偽隨機性在於：從該家族中隨機選擇的函數 （根據特定分佈），在給定預言機存取權限 (oracle access) 的情況下，無法被高效地與一個均勻隨機函數 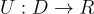區分開來。也就是說，對於實驗開始時選擇的某個固定鑰匙 s，對手可以自適應地查詢不同的值 ，以接收答案 ，而這些值 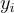，應該看起來是均勻隨機且獨立的（即使它們實際上是從種子 s 和輸入 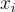確定性地計算出來的）。一個候選 PRF 族的例子是 AES-128，其中 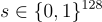且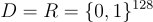

事實上，AES 族中的每個函數實際上是 上的一個 雙射 (bijection)，並且知道 s 也允許高效計算 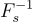，一般來說，PRF 不需要具備這些性質。

21.1 先前的 PRF 構造 (Previous PRF constructions):
GGM 給出了 PRF 的第一個形式化定義和第一個可證明安全的構造，基於任何長度倍增偽隨機生成器 (PRG) 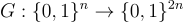，這樣的生成器可以從任何僅擴展單一位元的生成器構造而來。令 分別表示將 G 的輸出限制在其前半部分和後半部分。那麼對於 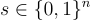和任何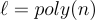

GGM PRF 定義為：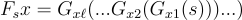

其中 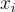表示 x 的第 i 個位元。換句話說：從鑰匙 s 開始，根據 PRF 輸入 x 的位元指示，反覆應用 G，取其輸出的前半部分或後半部分。請注意，此函數是高度 順序性 (sequential) 的：其電路深度與 PRF 輸入長度 ℓ 成正比。

Naor 和 Reingold (以及 Rosen) [NR95, NR97, NRR00] 基於一個他們稱之為 合成器 (synthesizer) 的通用物件，給出了高度 平行 的 PRF 構造，甚至從特定的數論假設（如決策 Diffie-Hellman (DDH) 和因數分解問題的難度）給出了更低深度的 PRF。後者的構造定義為「子集乘積的指數」：對於輸入定義域 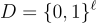，鑰匙由 ℓ 個元素 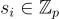和一個公開乘法群 G（階為 p) 的生成元 g 組成。一個輸入 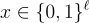，指定了子集乘積 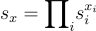，輸出則是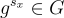

21.2 取整學習法與基於格的 PRF (Learning With Rounding and Lattice-Based PRFs)
決策-LWE (decision-LWE) 問題中固有的偽隨機性立即產生了一個 PRG，但其在輸入隨機性的使用上相當複雜且低效，因為它需要使用輸入位元從類高斯分佈中抽樣誤差。至於 PRF，GGM 構造抵消了 LWE 固有的良好平行性。這激發了人們去尋找基於格的 PRG 和 PRF 的替代構造。

取整學習法 (Learning With Rounding):
Banerjee、Peikert 和 Rosen (以下簡稱 BPR) [BPR12] 從格問題（即 LWE）構造了更高效的 PRG 和第一個非通用的 PRF。他們的第一個貢獻是一個稱為 取整學習法 (LWR) 的問題，它本質上是 LWE 的一個「去隨機化 (derandomized)」版本，其中誤差是確定性的。與 LWE 一樣，在 LWR 中有一個秘密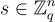

目標是將與 s 的「含噪」隨機內積與均勻隨機的區分開來。不同之處在於，在 LWR 中，樣本是作為 取整的 內積生成的：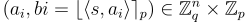

其中 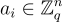是均勻隨機的，而 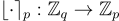（對於 p<q) 是模「取整函數」，定義為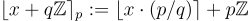

直觀上，在 LWE 中，關於內積的較不重要資訊被隨機小誤差隱藏，而在 LWR 中，相同的效果是通過確定性取整實現的。

BPR 證明，對於超多項式 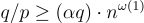。LWR 至少與模數 q 和錯誤率 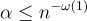的 LWE 一樣困難。有趣的是，LWR 很可能對於小得多的比率 q/p（其中 p 整除 q 以避免取整偏差）也是困難的，儘管目前還沒有基於最壞情況格問題的證明。注意到，Alwen 等人 [AKPW13] 和 Bogdanov 等人 [BGM+16] 的後續工作針對 有限 數量 m 的 LWR 樣本，根據比率 q/p 和基礎 LWE 錯誤率，在這個方向上取得了部分結果。這些結果對於某些應用的安全性是足夠的，但不幸的是對於 PRF 則不夠。

偽隨機函數 (Pseudorandom functions):
BPR 使用 LWR 問題來構造非常簡單且隨機性高效的 PRG，從而產生更實用的類 GGM PRF，以及非常簡單的對數深度 合成器 (synthesizers)，它們遵循 Naor 和 Reingold [NR95] 的範式產生多對數深度 (polylogarithmic-depth) PRF。最後，BPR 還給出了類似於 [NR97, NRR00] 中最低深度 PRF 構造的方案。該構造不是子集乘積的指數，而是一個 取整的 子集乘積，其中乘積是在一個秘密矩陣集合上進行的。更具體地說，對於定義域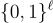

函數定義為：
容易驗證這個構造是「幾乎 (almost)」鑰匙同態的，因為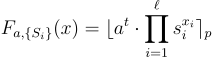

方程式 (21.1.1
其中秘密鑰匙（secret key）包含一個均勻隨機的 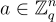和 ℓ 個短高斯分佈矩陣（short Gaussian-distributed matrices）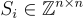

BPR 證明，在 LWE 假設下，這個函數是一個安全的 PRF，但僅適用於非常小的誤差率 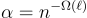，這導致需要一個相當大的模數 和維度 n，以及相應地大的鑰匙大小。

與 LWR 問題類似，即使對於更小的參數，例如一個足夠大且可被 p 整除的 q=poly(n)，方程式 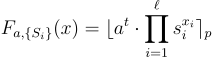中的函數也可能是一個安全的 PRF。雖然對於這些參數尚無已知的安全性證明，但也沒有已知的有效攻擊（除了對 LWE 的通用攻擊（generic attacks））。上述建構的基於環（ring-based）的類比方案的實際實例化和軟體實作已在 [BBL+14] 中給出。

21.3 鑰匙同態偽隨機函數 (Key-Homomorphic PRFs)
繼 [BPR12] 之後，Boneh 等人（以下簡稱 BLMR）[BLMR13] 首次利用晶格/LWE 給出了鑰匙同態偽隨機函數（KH-PRF）的標準模型建構。（在此之前，KH-PRF 的唯一建構是在隨機預言模型（random-oracle model）中 [NPR99]。）一個 KH-PRF 族是具有額外性質的 PRF 族 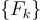。該性質是對於所有鑰匙 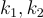和輸入 x，滿足 ，其中鑰匙空間和輸出範圍都被視為有限加法群（finite additive groups）。如 [NPR99, BLMR13] 所示，KH-PRF 有許多有用的應用，例如分散鑰匙分發中心（key-distribution center）的運作，以及可更新的對稱鑰匙加密（updatable symmetric-key encryption）。

在 BLMR 的構造中，秘密鑰匙（secret key）只是一個均勻隨機的向量 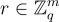，其中 m≈nlogq，並且有兩個短的（例如，二元的或高斯分佈的）隨機方陣 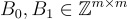。這些矩陣被視為所有鑰匙共用的共享隨機性（shared randomness）。或者，可以將這些矩陣視為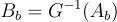
（對於某些公開的均勻隨機矩陣 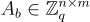），其中分解函數（decomposition function)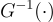
如方程式 (5.4.1) 所定義。與 BPR 的構造類似，對於輸入定義域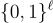

BLMR 函數被定義為四捨五入的子集乘積（rounded subset-product）：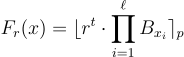
很容易驗證這個構造是「幾乎」鑰匙同態（”almost” key-homomorphic）的，因為 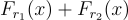和 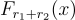。在每個座標上最多相差 1，這是由於兩種情況下的四捨五入順序不同所致。

BLMR 證明他們的構造在 n 維 LWE 假設下是一個安全的 PRF，適用於誤差率 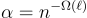，因此其參數與最低深度的 BPR 構造（方程式 (21.1.1)）的參數相當。證明中使用的主要思想是：具有「大」秘密
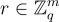和短公開矩陣 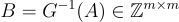的 LWE 問題，其困難度與維度 n≈m/logq 下的 LWE 問題相同。這是因為：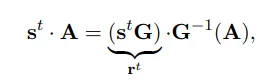

所以可以有效地將具有秘密 s 的常規 LWE 樣本轉換為上述形式。（同樣的思想已在許多其他工作和情境中使用，例如 [BV11b, MP12, BLP+13, GSW13]。）繼 [BLMR13] 之後，Banerjee 和 Peikert [BP14] 基於實質上更弱的 LWE 假設（例如，誤差率僅為 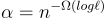。甚至 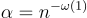給出了鑰匙同態 PRF，這帶來了更好的鑰匙大小（key size）和運行時間（runtime）。例如，鑰匙大小從 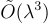位元減少到 位元，共享隨機性從 位元減少到 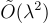位元，基於環的構造（ring-based constructions）也有類似的改進。這些改進的代價是並行性（parallelism）稍差，具體來說，是在函數的「公開可計算」（”publicly computable”）子集乘積部分的深度上增加了一個對數因子（logarithmic factor）。[] 中構造的主要思想是：不讓 PRF 輸入 x 定義短矩陣 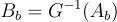的子集乘積，而是讓它通過預定義的矩陣乘法和 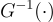分解的調度（scheduling）來定義一個矩陣 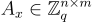。特別是，分解矩陣的乘積本身可以以嵌套方式（nested fashion）被分解。這在安全性證明中具有更好地控制誤差項擴張的效果，從而允許使用更小的參數。這些思想繼承自最近關於全同態加密（fully homomorphic encryption）和基於屬性的加密（attribute-based encryption）的文獻 [BV14, BGG+14, AP14]。

最後，提到 Banerjee 等人 [BFP+15] 以及 Brakerski 和 Vaikuntanathan [BV15] 最近的獨立工作，以不同的方式推廣了 [BP14] 的構造，給出了鑰匙同態限制性偽隨機函數（key-homomorphic constrained PRFs）。限制性 PRF（Constrained PRFs）由 [KPTZ13, BW13, BGI14] 這三篇同時且獨立的工作引入，它允許委派秘密鑰匙（delegation of secret keys），這些鑰匙允許在滿足特定謂詞（predicates）的輸入上計算 PRF，同時保持該函數在所有其他輸入上的偽隨機性（pseudorandomness）。

參考資料
[GGM84] O. Goldreich, S. Goldwasser, and S. Micali. How to construct random functions. J. ACM, 33(4):792–807, 1986. Preliminary version in FOCS 1984.

[BPR12] A. Banerjee, C. Peikert, and A. Rosen. Pseudorandom functions and lattices. In EUROCRYPT, pages 719–737. 2012.

[AKPW13] J. Alwen, S. Krenn, K. Pietrzak, and D. Wichs. Learning with rounding, revisited - new reduction, properties and applications. In CRYPTO, pages 57–74. 2013.

[BGM+16] A. Bogdanov, S. Guo, D. Masny, S. Richelson, and A. Rosen. On the hardness of learning with rounding over small modulus. In TCC, pages 209–224. 2016.

[NR95] M. Naor and O. Reingold. Synthesizers and their application to the parallel construction of pseudo-random functions. J. Comput. Syst. Sci., 58(2):336–375, 1999. Preliminary version in FOCS 1995

[NR97] M. Naor and O. Reingold. Number-theoretic constructions of efficient pseudo-random functions. J. ACM, 51(2):231–262, 2004. Preliminary version in FOCS 1997.

[NRR00] M. Naor, O. Reingold, and A. Rosen. Pseudorandom functions and factoring. SIAM J. Comput., 31(5):1383–1404, 2002. Preliminary version in STOC 2000.

[BBL+14] A. Banerjee, H. Brenner, G. Leurent, C. Peikert, and A. Rosen. SPRING: Fast pseudorandom functions from rounded ring products. In FSE, pages 38–57. 2014.

[BLMR13] D. Boneh, K. Lewi, H. W. Montgomery, and A. Raghunathan. Key homomorphic PRFs and
their applications. In CRYPTO, pages 410–428. 2013.

[NPR99] M. Naor, B. Pinkas, and O. Reingold. Distributed pseudo-random functions and KDCs. In EUROCRYPT, pages 327–346. 1999.

[BV11b] Z. Brakerski and V. Vaikuntanathan. Efficient fully homomorphic encryption from (standard) LWE. SIAM J. Comput., 43(2):831–871, 2014. Preliminary version in FOCS 2011.

[MP12] D. Micciancio and C. Peikert. Trapdoors for lattices: Simpler, tighter, faster, smaller. In EUROCRYPT, pages 700–718. 2012.

[BLP+13] Z. Brakerski, A. Langlois, C. Peikert, O. Regev, and D. Stehle. Classical hardness of learning with errors. In STOC, pages 575–584. 2013.

[GSW13] C. Gentry, A. Sahai, and B. Waters. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In CRYPTO, pages 75–92. 2013.

[BP14] A. Banerjee and C. Peikert. New and improved key-homomorphic pseudorandom functions. In CRYPTO, pages 353–370. 2014.

[BV14] Z. Brakerski and V. Vaikuntanathan. Lattice-based FHE as secure as PKE. In ITCS, pages 1–12. 2014.

[BGG+14] D. Boneh, C. Gentry, S. Gorbunov, S. Halevi, V. Nikolaenko, G. Segev, V. Vaikuntanathan, and D. Vinayagamurthy. Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In EUROCRYPT, pages 533–556. 2014.

[AP14] J. Alperin-Sheriff and C. Peikert. Faster bootstrapping with polynomial error. In CRYPTO, pages 297–314. 2014.

[BFP+15] A. Banerjee, G. Fuchsbauer, C. Peikert, K. Pietrzak, and S. Stevens. Key-homomorphic constrained pseudorandom functions. In TCC, pages 31–60. 2015.

[KPTZ13] A. Kiayias, S. Papadopoulos, N. Triandopoulos, and T. Zacharias. Delegatable pseudorandom functions and applications. In CCS, pages 669–684. 2013.

[BW13] D. Boneh and B. Waters. Constrained pseudorandom functions and their applications. In
ASIACRYPT, pages 280–300. 2013.

[BGI14] E. Boyle, S. Goldwasser, and I. Ivan. Functional signatures and pseudorandom functions. In PKC, pages 501–519. 2014.